Transformation Cont

对应GAMES101 Lecture 04

3D transformations[上一节]

3D变换

缩放(Scale)

$$S(s_x,s_y,s_z)=\left(\begin{array}{cccc}{s}_x& 0& 0& 0\\ \\ 0& s_y& 0& 0\\ \\ 0& 0& s_z& 0\\ \\ 0& 0& 0& 1\end{array}\right)$$

平移(Translation)

$$T(t_x,t_y,t_z)=\left(\begin{array}{cccc}1& 0& 0& t_x\\ \\ 0& 1& 0& t_y\\ \\ 0& 0& 1& t_z\\ \\ 0& 0& 0& 1\end{array}\right)$$

旋转绕轴[Rotation around x-, y-, or z-axis]

$$R_x(\alpha )=\left(\begin{array}{cccc}1& 0& 0& 0\\ \\ 0& \cos \alpha & -\sin \alpha & 0\\ \\ 0& \sin \alpha & \cos \alpha & 0\\ \\ 0& 0& 0& 1\end{array}\right)$$$$R_y(\alpha )=\left(\begin{array}{cccc}\cos \alpha & 0& \sin \alpha & 0\\ \\ 0& 1& 0& 0\\ \\ -\sin \alpha & 0& \cos \alpha & 0\\ \\ 0& 0& 0& 1\end{array}\right)$$$$R_z(\alpha )=\left(\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0& 0\\ \\ \sin \alpha & \cos \alpha & 0& 0\\ \\ 0& 0& 1& 0\\ \\ 0& 0& 0& 1\end{array}\right)$$

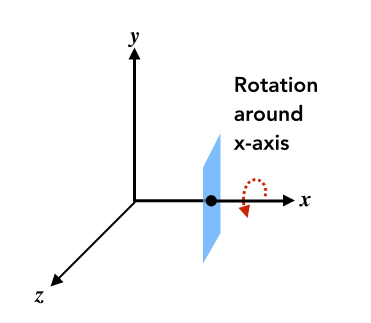
3D Rotations

Compose any 3D rotation from $R_x,R_y,R_z$ ?

$$R_{xyz}(\alpha ,\beta ,\gamma )=R_x(\alpha )R_y(\beta )R_z(\gamma )$$

• 欧拉角 (So-called Euler angles)
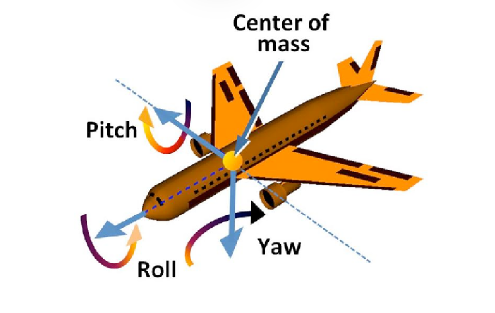
• 常用于飞行模拟器:滚转，俯仰，偏航 (Often used in flight simulators: roll, pitch, yaw)

Rodrigues’ Rotation Formula

Rotation by angle α around axis n

$$R(n,\alpha )=\cos (\alpha )I+(1-\cos (\alpha ))n{n}^T+\sin (\alpha )\underset{N}{\underbrace{\left(\begin{array}{ccc}0& -n_z& n_y\\ \\ n_z& 1& -n_x\\ \\ -n_y& n_x& 0\end{array}\right)}}$$

证明：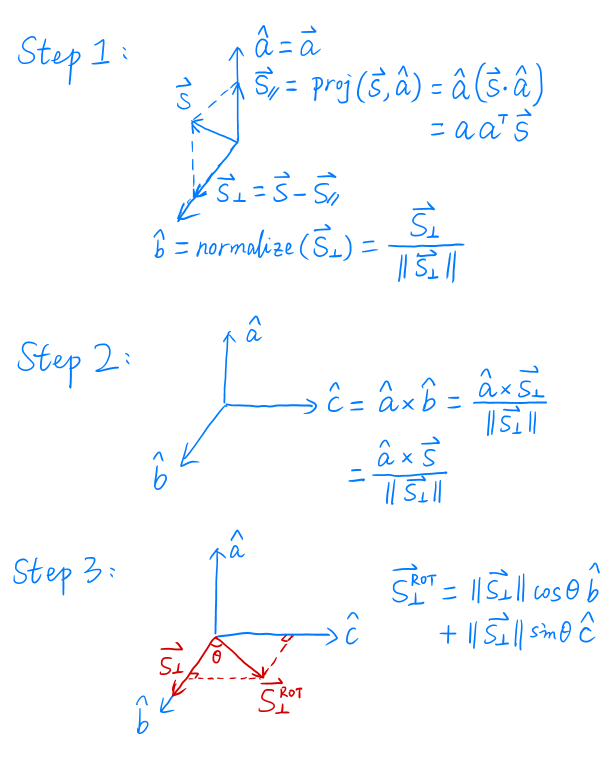

Viewing(观测) transformation

• View(视图)/Camera transformation
• Projection(投影) transformation
  • Orthographic(正交) projection
  • Perspective(透视) projection

视图/相机变换 (View/Camera transformation)

• 什么是观测变换? (What is view transformation?)

• 怎么实现? (How to perform view transformation?)

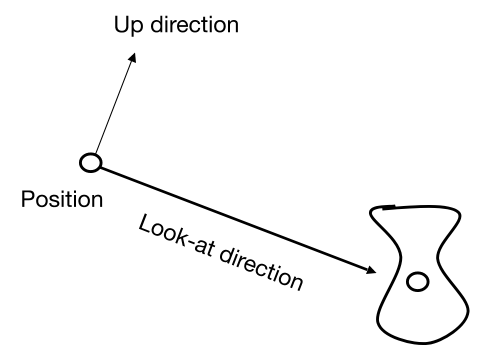
• 首先定义相机 (Define the camera first)

  • 位置 (Position) $\overrightarrow{e}$
  • 朝向 (Look-at / gaze direction) $\overrightarrow{g}$
  • 上方向(假设垂直于朝向) (Up direction(assuming perp. to look-at)) $\overrightarrow{t}$

• 关键 (Key observation)

  • 同时变换相对不变 (If the camera and all objects move together, the “photo” will be the same)

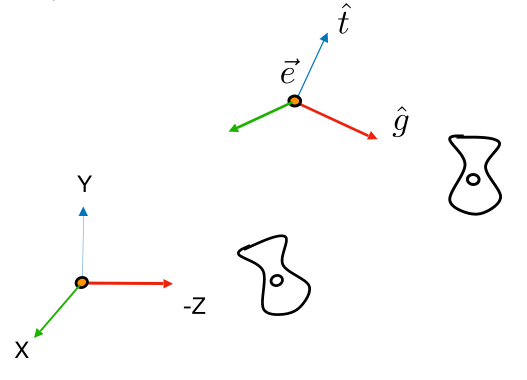
• 约定 (How about that we always transform the camera to)

  • 位于原点, Up在Y轴, 看向-Z轴 (The origin, up at Y, look at -Z)
  • 和相机一起变换物体 (And transform the objects along with the camera)

• 变换相机通过矩阵M (Transform the camera by $M_{view}$)

  • 位于原点，在Y上，看-Z (So it’s located at the origin, up at Y, look at -Z )

• 数学上矩阵M ($M_{view}$ in math?)

  • 移动e到原点 (Translates e to origin)
  • 旋转g到-Z (Rotates g to -Z)
  • 旋转t到Y (Rotates t to Y)
  • 旋转(g叉乘t)到X (Rotates (g x t) To X)

• 求最终矩阵
  • $M_{view}=R_{view}{T}_{view}$
  • 步骤一 (Translate e to origin)$$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ \\ 0& 1& 0& -x_y\\ \\ 0& 0& 1& -x_z\\ \\ 0& 0& 0& 1\\ \end{array}\right]$$
  • 步骤二 (Rotate g to -Z, t to Y, (g x t) To X)
  • 考虑逆旋转 (Consider its inverse rotation: X to (g x t), Y to t, Z to -g)$$R_{view}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ \\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ \\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ \\ 0& 0& 0& 1\\ \end{array}\right]$$WHY? 利用逆矩阵的性质，先算从原点到任意点再转置过来$$R_{view}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ \\ x_t& y_t& z_t& 0\\ \\ x_{-g}& y_{-g}& z_{-g}& 0\\ \\ 0& 0& 0& 1\\ \end{array}\right]$$
• 总结
  • 与相机一起变换物体 (Transform objects together with the camera)
  • 直到相机在原点，在Y上，看-Z (Until camera’s at the origin, up at Y, look at -Z)

投影变换 (Projection Transformation)

• 计算机图形学中的投影 (Projection in Computer Graphics)
  • 3D to 2D
  • 正交投影 (Orthographic projection)
  • 透视投影 (Perspective projection)

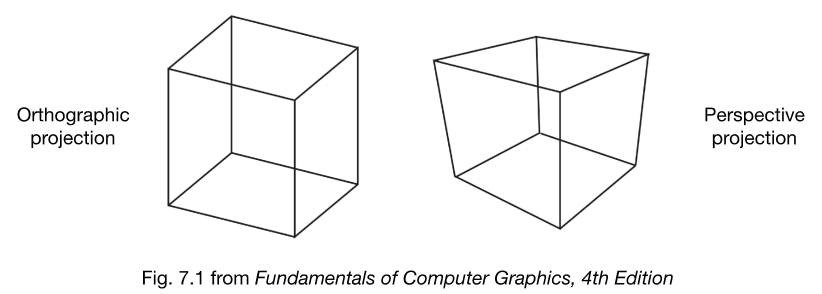
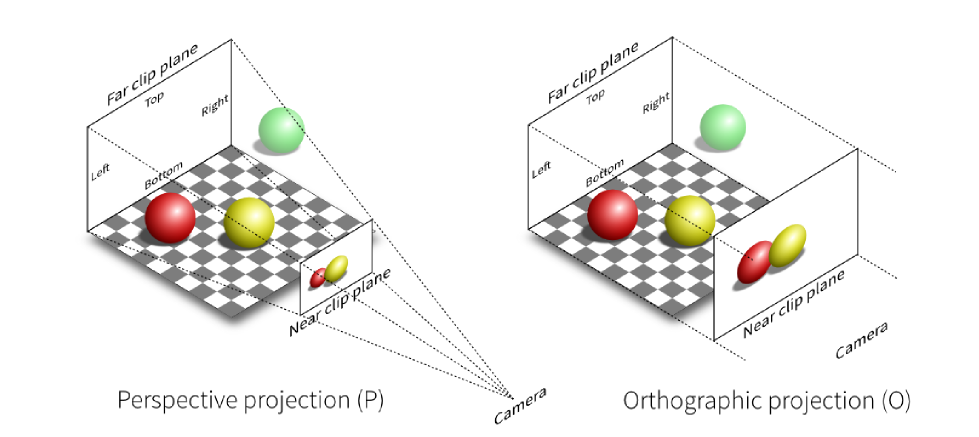
正交投影 (Orthographic Projection)

简单理解

• 相机位于原点，看着-Z，向上看Y
• 去掉Z轴
• 将得到的矩形平移并缩放为[- 1,1]² (Translate and scale the resulting rectangle to [-1, 1]²)

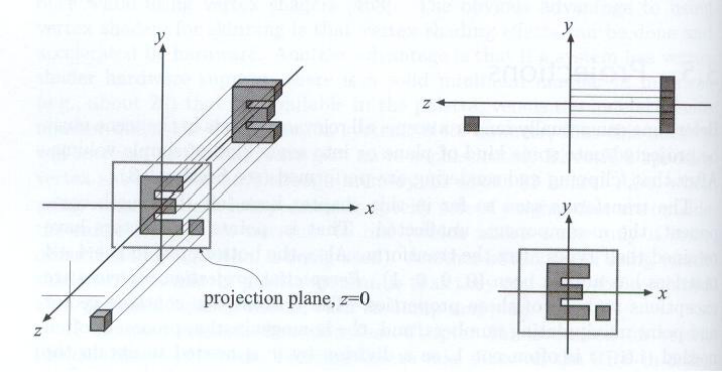
通常来说 (In general)

• We want to map a cuboid [l, r] x [b, t] x [f, n] to the “canonical (正则、规范、标准)” cube [-1, 1]³

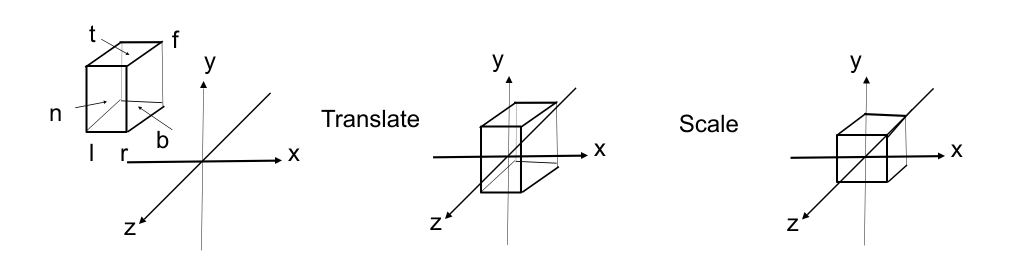
Slightly different orders (to the “simple way”)

• Center cuboid by translating
• Scale into “canonical” cube

平移矩阵(Transformation matrix)

• Translate (center to origin) first, then scale (length/width/height to 2)

$$M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ \\ 0& \frac{2}{t-b}& 0& 0\\ \\ 0& 0& \frac{2}{n-f}& 0\\ \\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ \\ 0& 1& 0& -\frac{t+b}{2}\\ \\ 0& 0& 1& -\frac{n+f}{2}\\ \\ 0& 0& 0& 1\end{array}\right]$$

Caveat

• Looking at / along -Z is making near and far not intuitive (n > f)
• FYI: that’s why OpenGL (a Graphics API) uses left hand coords

透视投影 (Perspective Projection)

最常见于计算机图形学、美术、视觉系统, 进大远小, 更符合人眼观测

开始之前, 回想一下齐次坐标的性质

• (x, y, z, 1), (kx, ky, kz, k != 0), (xz, yz, z², z != 0) all represent the same point (x, y, z) in 3D
• e.g. (1, 0, 0, 1) and (2, 0, 0, 2) both represent (1, 0, 0)

怎么做(How to do perspective projection)

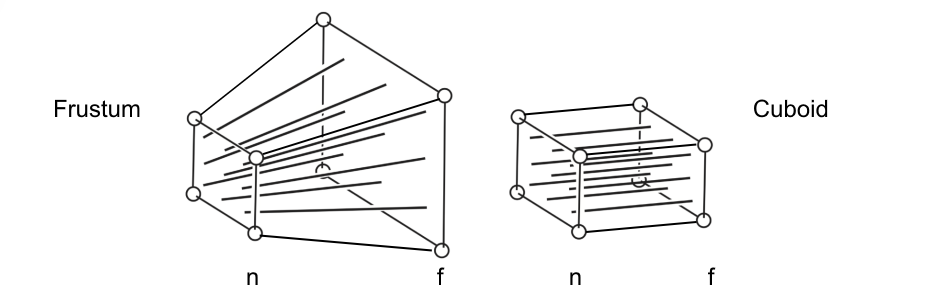
• 首先把截锥体压成一个长方体 (First “squish” the frustum into a cuboid[n->n, f->f][$M_{persp\to ortho}$])
• 做正交投影 (Do orthographic projection[$M_{ortho}$, already known!])

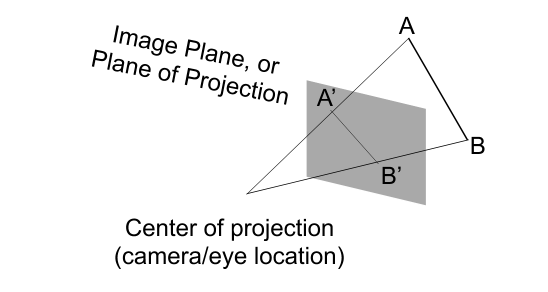
找对应点之间的关系

Find the relationship between transformed points (x’, y’, z’) and the original points (x, y, z)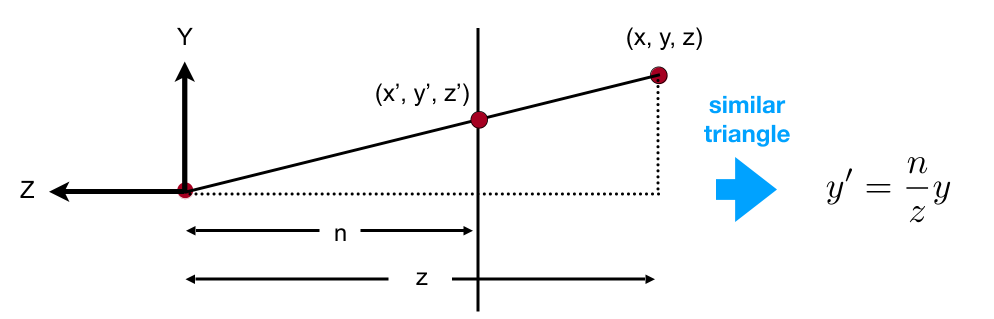

• 齐次坐标系下 (In homogeneous coordinates)

$$\left(\begin{array}{c}x\\ \\ y\\ \\ z\\ \\ 1\end{array}\right)\Rightarrow \left(\begin{array}{c}nx/z\\ \\ ny/z\\ \\ unknown\\ \\ 1\end{array}\right)==\left(\begin{array}{c}nx\\ \\ ny\\ \\ stillunknown\\ \\ z\end{array}\right)$$

• So the “squish” (persp to ortho) projection does this

$$M_{persp\to ortho}^{4\times 4}\left(\begin{array}{c}x\\ \\ y\\ \\ z\\ \\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ \\ ny\\ \\ unknown\\ \\ z\end{array}\right)$$

• Already good enough to figure out part of $M_{persp\to ortho}$

$$M_{persp\to ortho}=\left(\begin{array}{cccc}n& 0& 0& 0\\ \\ 0& n& 0& 0\\ \\ ?& ?& ?& ?\\ \\ 0& 0& 1& 0\end{array}\right)$$

• 求第三行
  • Observation: the third row is responsible for z’
  $$M_{persp\to ortho}^{4\times 4}\left(\begin{array}{c}x\\ \\ y\\ \\ z\\ \\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ \\ ny\\ \\ unknown\\ \\ z\end{array}\right)\underrightarrow{replace-z-with-n}\left(\begin{array}{c}x\\ \\ y\\ \\ z\\ \\ 1\end{array}\right)\Rightarrow \left(\begin{array}{c}x\\ \\ y\\ \\ z\\ \\ 1\end{array}\right)==\left(\begin{array}{c}nx\\ \\ ny\\ \\ n^2\\ \\ n\end{array}\right)$$
  • So the third row must be of the form (0 0 A B)
  $$\left(\begin{array}{cccc}0& 0& A& B\end{array}\right)\left(\begin{array}{c}x\\ \\ y\\ \\ n\\ \\ 1\end{array}\right)=n^2$$$$An+B=n^2$$$$\left(\begin{array}{c}0\\ \\ 0\\ \\ f\\ \\ 1\end{array}\right)\Rightarrow \left(\begin{array}{c}0\\ \\ 0\\ \\ f\\ \\ 1\end{array}\right)==\left(\begin{array}{c}0\\ \\ 0\\ \\ f^2\\ \\ f\end{array}\right)$$$$Af+B=f^2$$$$A=n+f$$$$B=-nf$$
  • 最后再做一次正交投影
  $$M_{persp}=M_{ortho}{M}_{persp\to ortho}$$

结尾

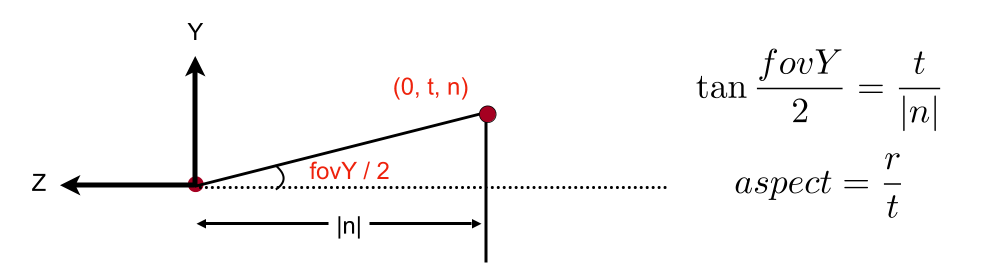
• What’s near plane’s l, r, b, t then?
  • If explicitly specified, good
  • Sometimes people prefer: vertical field-of-view (fovY) and aspect ratio(assume symmetry i.e. l = -r, b = -t)

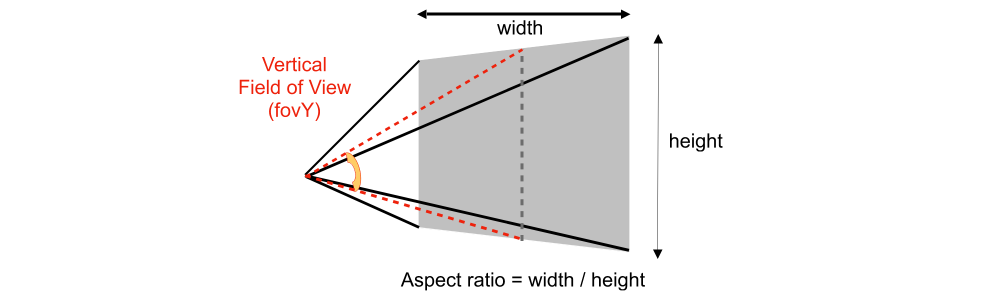
• How to convert from fovY and aspect to l, r, b, t?