几何

Mesh Operations: Geometry Processing (网格操作:几何处理)

• Mesh subdivision (细分)
• Mesh simplification (简化)
• Mesh regularization (规范化)

• Mesh Subdivision (upsampling) (网格细分(上采样))

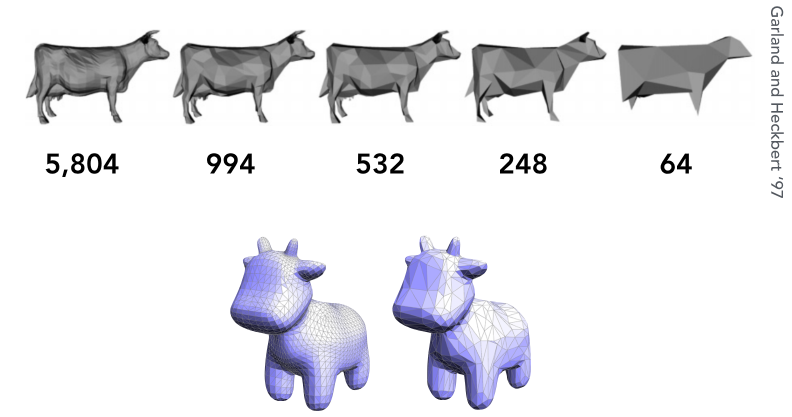
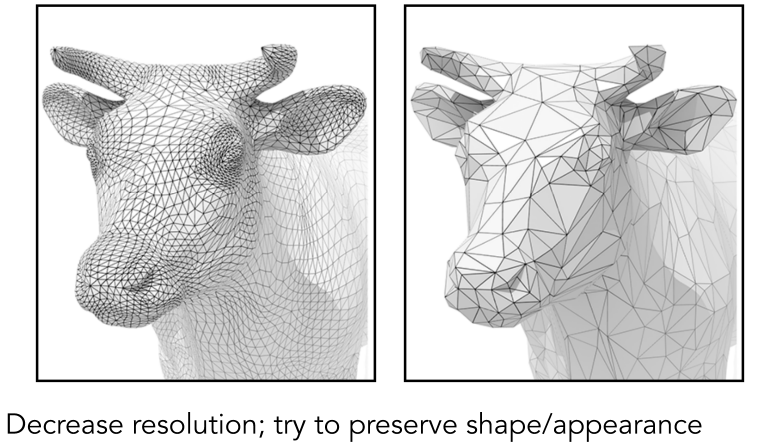
• Mesh Simplification (downsampling) (网格简化(下采样))

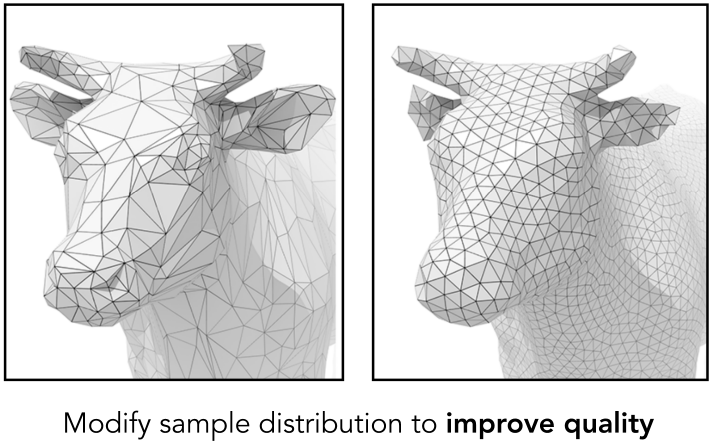
• Mesh Regularization (same #triangles) (网格正则化(相同的#三角形))

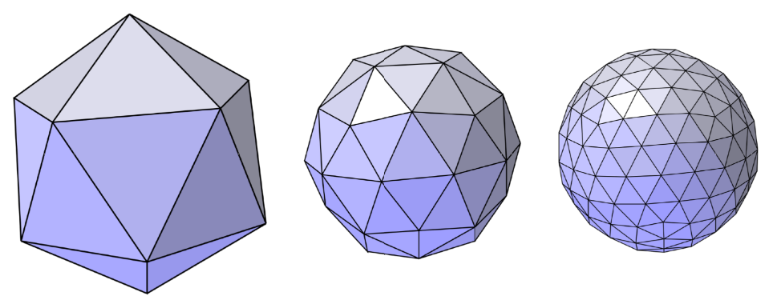
Subdivision (细分)

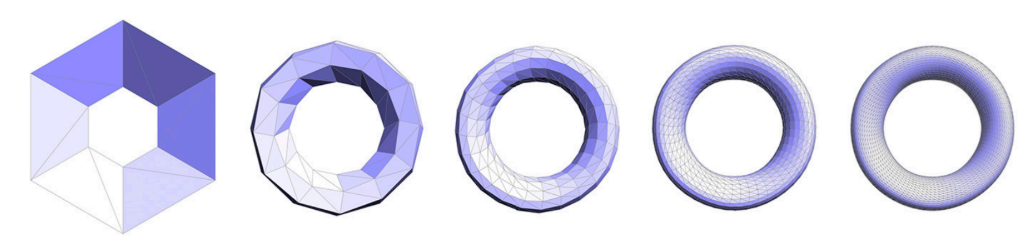
Loop Subdivision (循环细分)

Common subdivision rule for triangle meshes. First, create more triangles (vertices). Second, tune their positions

(三角网格的常用细分规则 首先，创建更多的三角形(顶点) 第二，调整他们的位置)

• Split each triangle into four
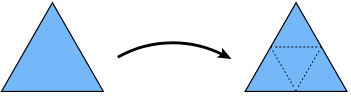
• Assign new vertex positions according to weights (根据权重分配新的顶点位置)
  • New / old vertices updated differently (新/旧顶点更新方式不同)

Loop Subdivision — Update

For new vertices: 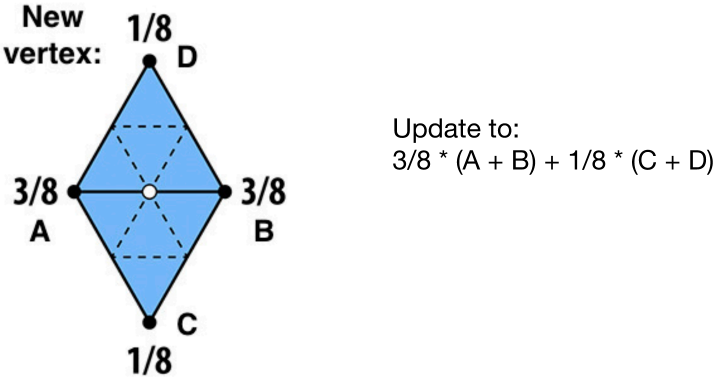For old vertices (e.g. degree 6 vertices here):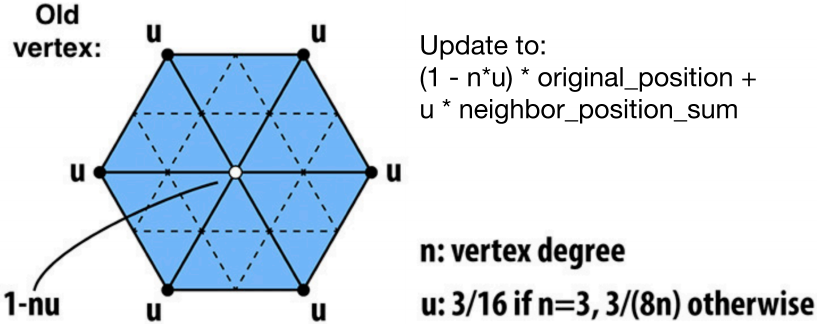

Catmull-Clark Subdivision (General Mesh) (Catmull-Clark细分(通用网格))

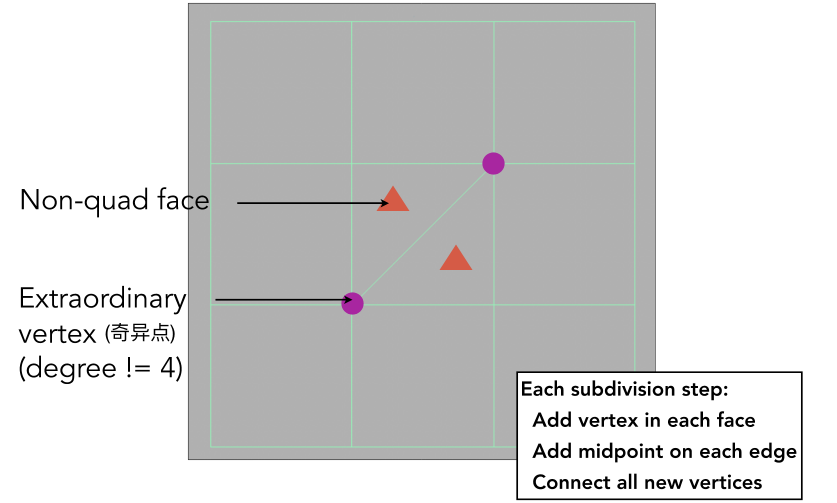
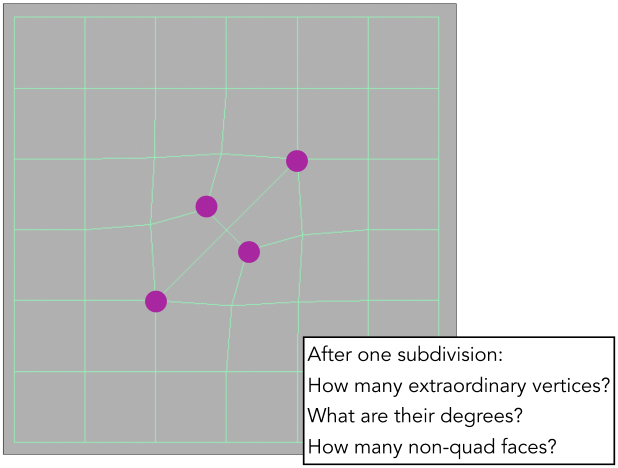
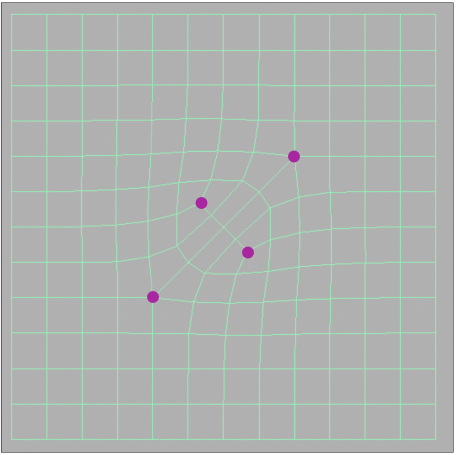
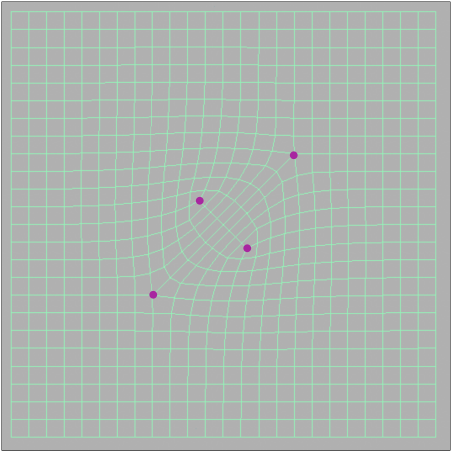
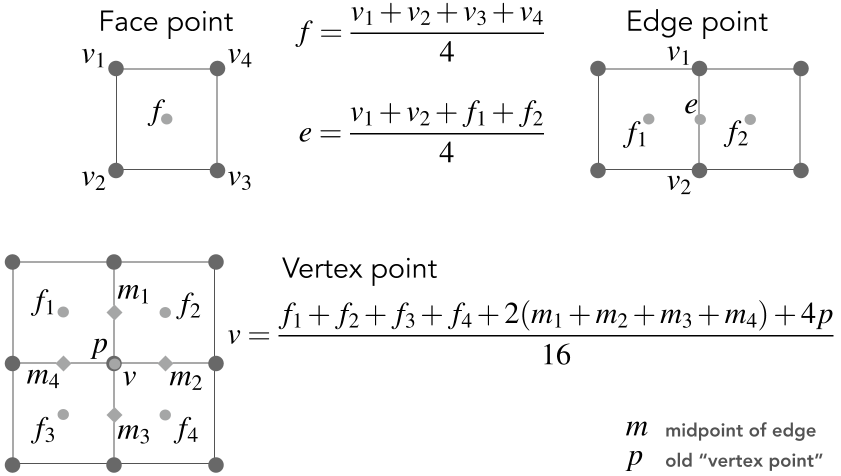
FYI: Catmull-Clark Vertex Update Rules (Quad Mesh) (供参考:Catmull-Clark顶点更新规则(四边形网格))

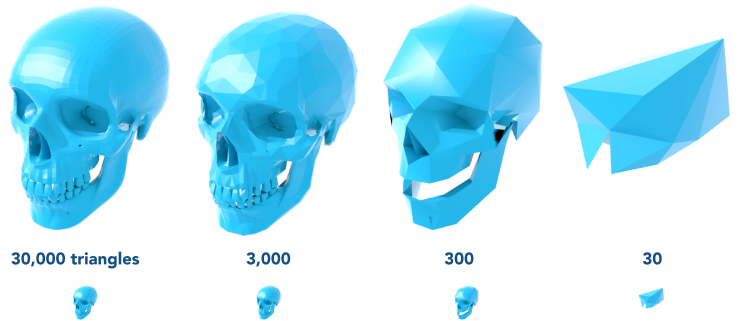
Simplification (简化)

Goal: reduce number of mesh elements while maintaining the overall shape (目标: 在保持整体形状的同时减少网格元素的数)

距离模型远时效果相差不大, 可根据需求进行选择

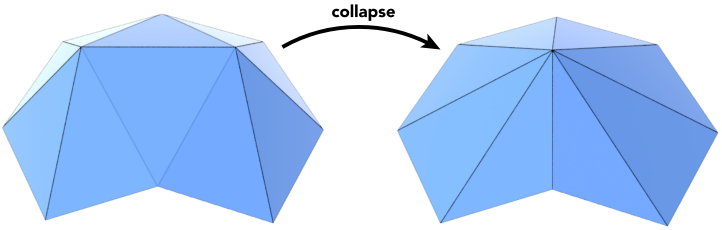
Collapsing An Edge (坍塌一条边)

• Suppose we simplify a mesh using edge collapsing (假设我们使用边缘折叠来简化一个网格)

边坍缩面临的问题:

• 坍缩哪些面？
• 如果优先坍缩不重要的面，那如何界定不重要？
• 坍缩后的顶点位置如何描述

Quadric Error Metrics (二次误差度量)

• How much geometric error is introduced by simplification? (化简会带来多少几何误差?)
• Not a good idea to perform local averaging of vertices (执行顶点的局部平均不是一个好主意)
• Quadric error: new vertex should minimize its sum of square distance (L2 distance) to previously related triangle planes! (二次误差:新的顶点应该最小化它的平方距离(L2距离)的总和之前相关的三角形平面!)

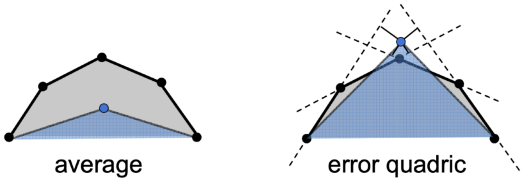
Quadric Error of Edge Collapse (边塌缩的二次误差)

• How much does it cost to collapse an edge?
• Idea: compute edge midpoint, measure quadric error
• Better idea: choose point that minimizes quadric error

Quadric Error Mesh Simplification